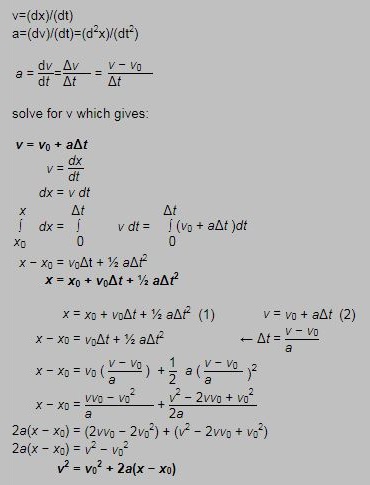Air Cannon Projectile Motion
WARNING: No Liability Is Assumed By The Developers Of This Website and All Literature Is Provided Second Hand, Use It At Your Own Risk!
Air Cannons and the Equations for Projectile Motion
How to calculate
| x acceleration | ax=0 |
| y acceleration | ay=-gravity=-9.8 m/s2 |
| x velocity | vx=v0cosθ |
| y velocity | vy=v0sinθ+ayt |
| x position | x=x0+v0xt |
| y position | y=y0+v0yt+(1/2)ayt2 |
(Work that shows the derivation of these equations are shown below)
From these equations you can easily find how far your projectile will go. Keep in mind that this is in ideal conditions such as a particle in space. Variances in recoil resistance and drag on your projectile will occur so your results will vary accordingly. In other words the distance your projectile actually goes will be less than what you predicted due to drag. Projectile drag calculations can get extensive and are therefore left out in this example.
Example problem:
You fire a projectile from a air cannon being held 1.5 meters from the ground at an angle of 42°. Using a chronograph you know that the velocity of the projectile leaving the barrel was 115 meters/second. How long was the projectile in the air for? How far will your projectile fire? What was the maximum height of the projectile? What was the projectile's speed on impact?
v0=115 m/s
θ=42°
y0=1.5 m
Find:
t, x, ymax and |v| at impact under the given conditions
Solution:
v0x=115 cos(42) = 85.4617 m/s
v0y=115 sin (42) = 76.9500 m/s
y=y0+v0yt+(1/2)ayt2 plug in values:
0=1.5+76.95t+(1/2)(-9.8)t2 solve for t.
t= 15.7236 seconds. So the projectile was in the air for 15.7236 seconds
now use x=x0+v0xt and plug in values:
x=0+85.4617 * 15.7236 = 1343.7656 meters. So the projectile will go 1343.7656 meters if
there was no drag or friction present.
Remember that the vertical velocity is zero when the projectile is at its highest point. 0=76.95-9.8*t solve for t, t=7.8520 seconds.
Now put that time into the y position equation:
y=y0+v0yt+(1/2)ayt2 plug in known value:
y=1.5+76.95t-(1/2)(9.8)t2 = 303.6073 meters. So the projectile goes 303.6073 meters high
vx= 85.4617 m/s, vy = 76.95 - 9.8t = -77.1413 m/s (where t=15.7236 seconds from above) square root of (vx2 + vy2) gives square root of (85.46172+ -77.14132)=36.8721 m/s
So the projectile strikes the ground at 36.8721 m/s.
Here is a nice little program that will give you an idea for the motion of you projectile: http://galileoandeinstein.physics.virginia.edu
Derivation of Projectile Motion Equations:
From calculus we know that velocity is the rate of change of displacement, and acceleration is the rate of change of velocity:
From these we can derive the following:
| x acceleration | ax=0 |
| y acceleration | ay=-gravity=-9.8 m/s2 |
| x velocity | vx=v0cosθ |
| y velocity | vy=v0sinθ+ayt |
| x position | x=x0+v0xt |
| y position | y=y0+v0yt+(1/2)ayt2 |