Air Cannon How to Calculate Recoil Conservation of Linear Momentum
WARNING: No Liability Is Assumed By The Developers Of This Website and All Literature Is Provided Second Hand, Use It At Your Own Risk!
The recoil force or kick from a launcher can be calculated using the principle of conservation of linear momentum. The recoil force you will experience while firing a launcher depends on the mass of the projectile, mass of the launcher, and velocity that the projectile leaves the barrel.
The linear momentum of a rigid object in this case is equal to the mass of the object multiplied by its velocity. If we set the sum of the system's linear momentums equal to the other system's sum of linear momentums then we have conservation of linear momentum as shown:
(Σ Syst. linear momentum)1 = (Σ Syst. linear momentum)2
As shown in the figure below, the projectile and launcher have been considered as a single system, since the impulsive forces, F, between the launcher and projectile are internal to the system and will therefore cancel from the analysis. So during the time it takes for the projectile to leave the barrel, Δt (about 0.03 seconds), the handles which are attached each exerts a nonimpulsive force Fs on the launcher. This is because Δt is very short, so that during this time the launcher only moves through a very small distance. As a result, Fs = ks 0, where k is the stiffness of the launchers support (much like a spring stiffness).
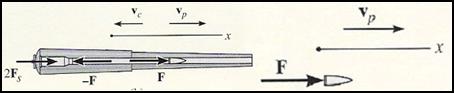
Schematic of projectile being fired (Reproduced without the permission of Engineering Mechanics and Dynamics, R.C. Pearson Prentice Hall, Upper Saddle River, NJ)
From this it is shown that momentum for the system is conserved in the horizontal direction.
In order to find out the recoil force, we first need to find what speed the launcher is recoiling at. Using the diagram above, we can write the equation for conservation of linear momentum for the launcher:
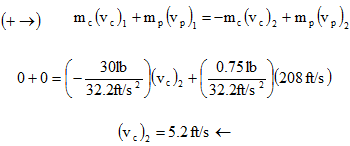
Where
- mc = Mass of cannon = weight of launcher divided by earth's gravity acceleration
- mp = Mass of projectile =weight of projectile divided by earth's gravity acceleration
- vc 2 = Velocity of cannon/launcher
- vp 2 = Velocity or speed that the projectile leaves the barrel.
This can be estimated but later verified with a chronograph or similar device
So this shows that the launcher is moving back at a speed of 5.2 feet per second.
The average impulsive force exerted by the launcher on the projectile can be determined
by applying the principle of linear impulse and momentum to the projectile (or to the launcher).
Using the principles of linear impulse for a rigid body we can write, >>
Where
Favg = Recoil force
Δt = Time it takes for projectile to leave the barrel
NOTE: Using these equations you can try different projectile weights and see how it affects the recoil of your launcher.